Через любую точку пространства

Поэтому предположение неверное, и прямые a и b не имеют общих точек. Согласно следствию из аксиом стереометрии, через прямую а и точку М проходит плоскость, и притом только одна. Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. А по третьей аксиоме, существует прямая MN, по которой пересекаются эти две плоскости.
В области параллельных прямых работало очень много ученых: Н. Наш сегодняшний урок начнем с того, что повторим, что же такое параллельные прямые. Teорема 1. Через две параллельные прямые можно провести плоскость, и притом только одну. Теорема 2. Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.

Теорема 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Теорема 4.
Две прямые, параллельные третьей прямой, параллельны. Обратите внимание! Здесь очень важны слова «лежат в одной плоскости». Потому что в пространстве бывают другие, НЕ параллельные прямые, которые тоже НЕ пересекаются. Вот, например, есть две прямые — a и b. Через них никак нельзя провести плоскость, но они и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. Прямые в пространстве параллельны, если лежат в одной плоскости и не пересекаются. Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются не имеют общих точек. Но второй случай допускает две возможности: прямые лежат в одной плоскости параллельны или прямые не лежат в одной плоскости.
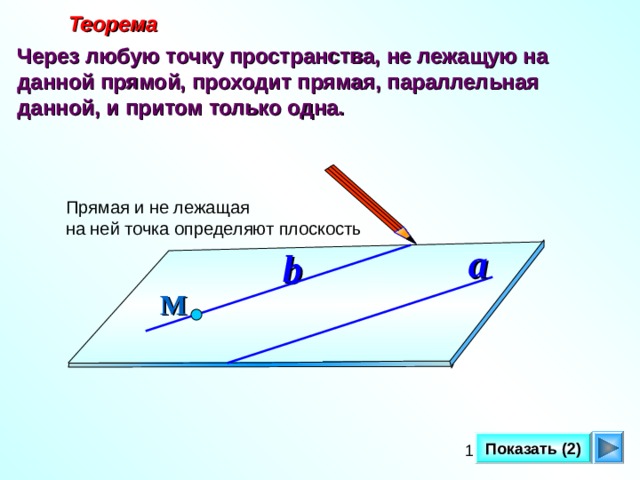
В первом случае они параллельны, а во втором — такие прямые называются скрещивающимися. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p. Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Если две прямые параллельны третьей прямой, то они параллельны. Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Из этого следует, что возможны три расположения прямой и плоскости:. Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка — она параллельна плоскости пола. Прямая и плоскость параллельны, если они не пересекаются, сколько бы их ни продолжали.
И представь себе, существует признак параллельности прямой и плоскости. Давай его сформулируем. Можно сказать и немного другими словами, но смысл остается тот же. Плоскости называются параллельными, если они не пересекаются, сколько бы их не продолжали.
И так же, как для прямой и плоскости, есть признак параллельности плоскостей. Его формулировка немного длиннее. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны. Наверное, для объяснения понадобилось очень много слов? Название, конечно, красивое, но непонятное! О чем же пойдет речь? И есть ответ: правда!
Ну вот, мы с вами обсудили определения и признаки параллельности прямых и плоскостей и даже немножко порисовали транзитивности. А теперь, когда урок подходит к концу, еще раз вкратце повторим то, о чем мы сегодня говорили, подведя итоги. Мы доказали теорему — Признак параллельности прямых: если две прямые параллельны третьей прямой, то они параллельны. Это мы знали еще из курса планиметрии, но это утверждение справедливо и для трех прямых в пространстве.
Мы доказали лемму о пересечении плоскости параллельными прямыми. На этом уроке мы рассмотрели параллельные прямые в пространстве. А именно, рассмотрели параллельность трех прямых. Доказали лемму о том, что если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
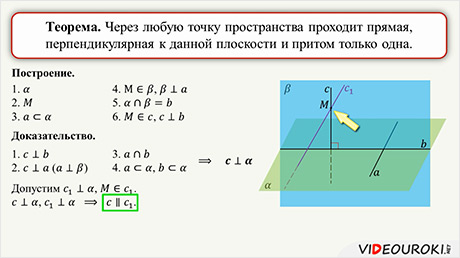
А затем с ее помощью доказали теорему о двух прямых, параллельных третьей прямой. Согласно аксиомам, если две точки прямой находятся в некоторой плоскости, то прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:. Прямая и плоскость называются параллельными, если они не имеют общих точек. Теорема 3. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Доказательство проведем от противного. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся. Мы пришли к противоречию. Следующие две теоремы очень часто используются при решении задач.
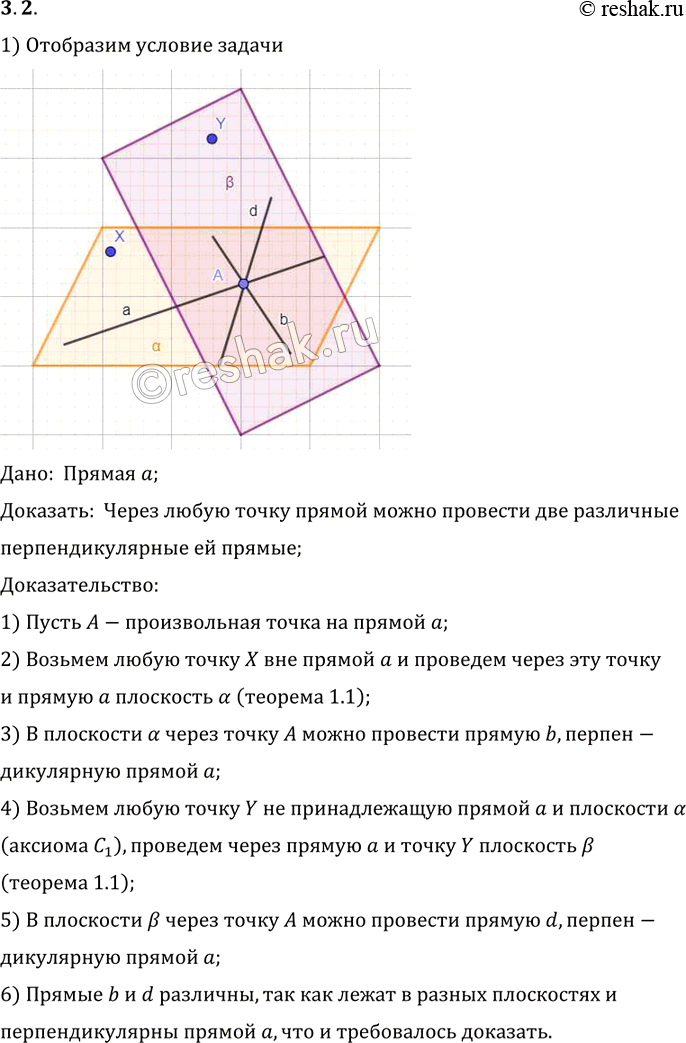
Теорема 4. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема 5. Если одна из двух параллельных прямых параллельная данной плоскости, то другая прямая либо так же параллельная данной плоскости, либо лежит в этой плоскости. Search this site. Параллельность прямых, прямой и плоскости. Доказательство: 1. Точку пересечения прямых a и c обозначим за K. Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L. Выводы: 1 Любые две прямые пучка параллельных прямых параллельны между собой. Пример: Одна сторона параллелограмма пересекает плоскость.
Параллельность прямой и плоскости Согласно аксиомам, если две точки прямой находятся в некоторой плоскости, то прямая лежит в этой плоскости.
- Фильмы Про Любовные Треугольник
- Как Влюбляются Разные Знаки Зодиака Мужчины
- Конспект По Статье Добролюбова Что Такое Обломовщина
- Встретила Бывшего Через 10 Лет
- Фильмы Про Возрастную Любовь
- Любовь Смешные Картинки
- Как Влюбить В Себя Мужа Ислам
- Любимому Мужу Прикольные Картинки
- К Чему Снится Любовник
- Обряд Сучий Волос На Любовь