Головоломка с точками, 9 точек 4 линии

Какое наибольшее количество точек можно зачеркнуть одной прямой линией? Удивительные 3 легенды и игра для детей. Вспомнить будущее.
И это будет также правильной разгадкой, хоть и максимально нестандартной. Честно говоря, иногда сложно представить, как человек может додумываться до некоторых идей. Например: одному из тех, кто пытался разгадать задачу, удалось соединить 9 точек при помощи 3 линий. Как он это сделал? Провел три линии в виде знака молнии через каждые три точки по горизонтали — и вуаля, решение нестандартное, но верное.
В условии также написано, что «проводить линии следует, не отрывая ручку от листа», поэтому некоторые хитрецы умудрялись положить ручку на бок и передвигали ее таким образом, что получилось провести три параллельных линии, соблюдая все правила.
Логические задачки 9 ноября Как соединить 9 точек четырьмя прямыми линиями? Условие задачи: все не так просто, как может показаться на первый взгляд На листе нарисованы 9 точек, расположенных в виде квадрата.
Также существуют некоторые ограничения, которых нужно придерживаться: все линии должны быть прямыми; линии не должны повторяться и возвращаться по уже прорисованному маршруту. Способы решения: а есть ли они? Между 9 точками можно провести ровно двадцать линий, из которых: две диагонали; четыре границы квадрата; шесть линий, которые соединяют центры сторон основного квадрата; восемь линий, которые соединяют центры сторон основного квадрата с его углами. Для решения этой головоломки нужно вспомнить два правила: Если есть две точки, через них проводится только 1 линия.
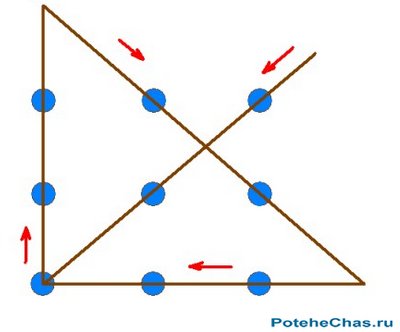
Прямая линия не имеет начала и конца, поэтому при решении задачи не нужно ограничиваться только девятью установленными точками. Итак, один из самых распространенных вариантов решения: Начинаем рисовать первую линию: проводим ее через цифры 1, 4 и 7 вниз по вертикали. Здесь же не отрывая руки, в голове представляем, что под семеркой есть еще одна цифра и доводим линию до нее, выходя за рамки квадратного полотна. После того, как линия была продолжена, двигаемся по диагонали в правую сторону наверх, соединяя точки 8 и 6.
Здесь мы тоже не останавливаемся и продолжаем рисовать линию, которая остановится напротив цифры 3. Как только точка установлена, рисуем прямую справа налево, соединяя точки 3, 2 и 1. Останавливаемся на единице. Далее дело за малым: проводим завершающую четвертую линию через точку 1, 5 и 9. Другие способы решения: ищем нестандартный подход Благодаря тем, кто подошел к решению данной загадки творчески, мы имеем более 12 вариантов решения этой головоломки, и все они выходят за рамки стандартного мышления.
А на что способно ваше мышление, чтобы решить эту головоломку нестандартным путем? Математика и логика для детей лет. Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате. Логическая загадка любой сложности заставит вас подумать о давно забытых предметах, вспомнить содержание детских сказок и смириться с тем, что ваш ребенок находит ответы быстрее вас.
Хотите проверить? Мы подготовили специальную подборку сложных логических загадок! Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. Люди стали мыслить по-другому?
Или дело в другом? Давайте разбираться вместе! Головоломка звучит так: «Соедините девять прямо расположенных точек ломаной линией, состоящей из четырех отрезков, не отрывая руки».
Задержитесь на мгновение! Подумайте самостоятельно! Это реально интересно решить самому. Эту задачку многие знают как «головоломка с девятью точками» или «очаровательная головоломка про 9 точек». Впервые ее опубликовали в году в журнале про шахматы Le Sphinx. Задал ее французский шахматист Сэм Лойд. Как потом оказалось, он станет автором различных математических головоломок. Но именно эта будоражит умы до сих пор.
Официально в Энциклопедию ее внесли в году.
Это сделал сын шахматиста, который получил имя в честь своего отца, то есть он был тоже Сэмом Лойдом. Так как точки на столе изображали яйца, то в Энциклопедии эта задача стала «Головоломкой с яйцом Колумба».
Почему Колумба? Ответ вы можете прочитать в статье о «колумбове яйце» — ссылка на неё будет в конце статьи. Ну ладно, давайте перейдем непосредственно к решению этой головоломки. Решение в 4 вариантах листайте галерею вправо :.
Также есть решение очень похожее на предыдущее и оно тоже в 4 вариантах листайте галерею вправо :. Все эти решения истинно правильные. Но… откуда тогда взялись ещё варианты решения данной задачи? Написать про эту математическую головоломку меня натолкнул спор, который был весьма горячим и завел нас в учебник геометрии, в определения «отрезка», «прямого отрезка» и «ломаной линии, состоящей из прямых отрезков».
Но речь сейчас не об этом. А о том, как неправильная формулировка задачи дала толчок к появлению совершенно новых ответов, которые теперь по-своему правильны. Как мы знаем, чтобы не попасть под бан плагиатства многие начинают изменять слова, что в итоге искажает первоначальный смысл!
Так получилось и с этой задачей. Через лет головоломка стала звучать немного по-другому: «Как соединить 9 точек 4 линиями, не отрывая карандаша от бумаги?
Или еще лучше: «Соединить линиями 9 точек». Понятно, что решение здесь уже будет совсем другим.

Так как в этих условиях нигде не сказано, что линия должна быть ломанной и состоять из 4 отрезков — это и есть самое главное условие данной задачи! Но её упустили в угоду уникальности текста.
Решение при таком условии получается немного другим. Теперь можно возвращаться по одной и той же линии, так как из условия ушло главное — соединить точки ломаной линией, состоящей из 4-х самостоятельных отрезков. А именно ломанная линия не позволяет вернуться.

А если вы возвращаетесь, то это уже будет считаться как еще один самостоятельный другой отрезок! Убрали вроде всего два слова «ломаная линия», а смысл потерялся. И теперь, люди с пеной у рта доказывают, что такое решение тоже имеет место. И они правы! Какая задача, такой и ответ. Ну это решение шуточное и оно подразумевает под собой, что в головоломке точки жирные и практически кружочки.
Эту задачу сократили настолько, что практически ничего не осталось от первоначального условия. А поскольку требования о прямых в условии не было, то через девять точек можно провести и одну линию — это еще одно шуточное решение, которое очень даже может быть, при неправильно заданном условии. А если бумажный лист свернуть в трубочку чуть наискосок, то получится следующее решение:.